Superpolished Optics
This is Sections 10.1, 10.2, and 10.3 of the Laser Optics Resource Guide.
The desire to achieve higher throughput and lower loss in laser systems drives the need for optical components with minimal scatter, particularly in applications involving short wavelengths or high-power lasers. Optics that minimize scatter using ultra-low surface roughness are commonly referred to as “superpolished”. While no industry standard exists for what roughness qualifies an optic as superpolished, Edmund Optics® established a process for polishing optical surfaces to a root mean square (RMS) surface roughness of less than one angstrom (10-10 m) for parts-per-million-level scattering. These sub-angstrom, low-loss surfaces are ideal for precise laser applications including cavity ring-down systems and laser gyroscopes.
Superpolished optics also compliment low-loss coating technology such as ion beam sputtering (IBS). The spectral performance of these coatings, if skillfully deposited, is often limited by the roughness of their substrates.
Measuring Sub-Angstrom Surface Roughness
Every tool used for metrology has its own unique measurable spatial frequency range. Figure 1 displays the overlapping spatial frequency ranges of three different devices commonly used to measure surface errors: conventional interferometry, white light interferometry (WLI), and atomic force microscopy (AFM).
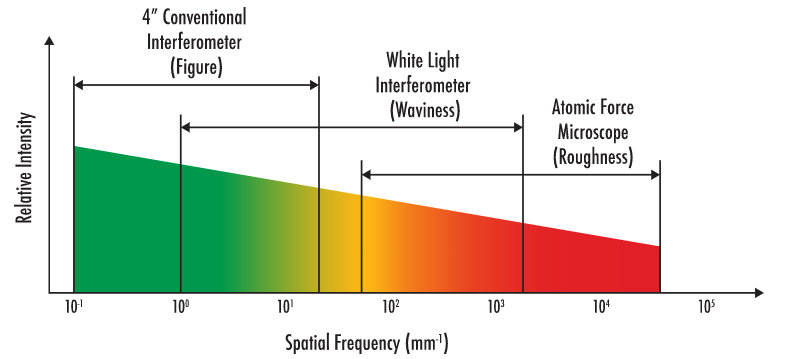
Figure 1: Measurable spatial frequency ranges of several metrology technologies, revealing overlapping capabilities1
Different spatial frequency ranges are classified as different categories of surface errors. These groups are not clearly defined frequency boundaries but are widely-accepted to cover certain general ranges. A conventional interferometer using a HeNe laser is well-suited for measuring figure error, which is low spatial frequency error associated with typical Zernike polynomials. The spatial frequency range of conventional interferometers slightly overlaps WLI’s mid-spatial frequency range, but WLI is still a better option for measuring waviness, which is a finer level of surface errors. Waviness begins to contribute to performance degradation from scatter. Both WLI and AFM can measure roughness, or higher spatial frequency errors, but application requirements determine the optimal instrument to use. Applications in the visible or IR spectra are generally measured at frequencies less than 2,000 cycles/mm, in which case WLI is an ideal metrology method. AFM is optimal for taking a closer look at an optic’s surface and can be necessary for UV applications, as higher spatial frequencies may need to be measured.
Increasing spatial frequency range typically comes at a tradeoff of a decreasing field of view. AFM can directly measure sub-angstrom surfaces, but a small field of view and high sensitivity make AFM more ideal for laboratory use rather than production environments. Data correlation between WLI and AFM, in tandem with steps to maximize the performance of the WLI, have allowed Edmund Optics® to confirm WLI as an effective tool for measuring sub-angstrom RMS surface roughness in a production setting.2
Manufacturing Superpolished Optics
Conventional optical polishing is a subtractive and iterative process where increasingly finer grits of abrasives are used to remove damage from an optical surface caused by earlier grinding and polishing stages. No matter how fine a grit is used, loose abrasive polishing will result in some level of subsurface damage. This damage at and below the optical surface increases surface roughness, energy absorption, and scatter, which generates heat and decreases system efficiency. Optical scatter is proportional to the surface roughness squared.
However, the superpolishing process developed by Edmund Optics eliminates subsurface damage by changing focus from a mechanical loose abrasive polishing process to the chemical reactions between the glass, slurry, and polishing lap. Mechanical force is only used to remove particles from the surface as reactions occur in the Beilby layer. Silica glass is insoluble in water, but during polishing a silica layer modified by the diffusion of hydroxyl ions is formed called the Beilby layer. Once this is formed it protects the optic from further change.3
Submersion polishing is used to create superpolished sub-angstrom roughness optics. A hydrated lap with slurry is kept at the same temperature as the substrate while temperature and pH level are highly controlled. This facilitates a chemical reaction while surface tension creates a protective barrier against contaminants.4
Superpolished Optics from Edmund Optics
Edmund Optics demonstrated that sub-angstrom optics could be repeatedly manufactured on planar fused silica substrates. No observable surface structure or subsurface damage were left behind on the optics from polishing (Tables 1 and 2).
| Fused Silica Optics Before Superpolishing | |||
| P-V (Å) | RMS (Å) | Ra (Å) | |
| Average | 183.42 | 7.42 | 5.70 |
| Range | 2089.92 | 18.24 | 11.19 |
| Standard Deviation | 186.88 | 2.91 | 1.82 |
Table 1: Substrate properties before submersion superpolishing.
| Fused Silica Optics After Superpolishing | |||
| P-V (Å) | RMS (Å) | Ra (Å) | |
| Average | 7.86 | 0.45 | 0.33 |
| Range | 1.13 | 0.03 | 0.10 |
| Standard Deviation | 0.98 | 0.02 | 0.02 |
Table 2: Submersion polishing for 2 hours proved to reduce RMS surface roughness from >7Å to <0.5 Å. More details may be found in our SPIE conference proceedings2,4
References
- Leslie L. Deck, Chris Evans, "High performance Fizeau and scanning whitelight interferometers for mid-spatial frequency optical testing of free-form optics," Proc. SPIE 5921, Advances in Metrology for X-Ray and EUV Optics, 59210A (31 August 2005); doi: 10.1117/12.616874
- Shawn Iles, Jayson Nelson, "Sub-angstrom surface roughness metrology with the white light interferometer," Proc. SPIE 11175, Optifab 2019, 1117519 (15 November 2019); https://doi.org/10.1117/12.2536683
- Finch, G. Ingle. “The Beilby Layer on Non-Metals.” Nature, vol. 138, no. 3502, 1936, pp. 1010–1010., doi:10.1038/1381010a0.
- Jayson Nelson, Shawn Iles, "Creating sub angstrom surfaces on planar and spherical substrates," Proc. SPIE 11175, Optifab 2019, 1117505 (15 November 2019); https://doi.org/10.1117/12.2536689
- Peter D. Groot, “The Meaning and Measure of Vertical Resolution in Optical Surface Topography Measurement.” Applied Sciences, 7(1), 54 (5 January 2017) doi:10.3390/app7010054
More Resources
- Ultra-Low Surface Roughness Polishing and Metrology Webinar Recording
- Trending in Optics: Superpolished Optics
- Metrology for Laser Optics
- Subsurface Damage
- Laser Optics Lab Video Series
- Metrology at Edmund Optics: Measuring as a Key Component of Manufacturing













 Previous Section
Previous Section 



or view regional numbers
QUOTE TOOL
enter stock numbers to begin
Copyright 2023, Edmund Optics Inc., 101 East Gloucester Pike, Barrington, NJ 08007-1380 USA
California Consumer Privacy Acts (CCPA): Do Not Sell or Share My Personal Information
California Transparency in Supply Chains Act