Introduction to Basic Ray Optics

Authors: Ian Schwartz

When an optical wave travels between mediums, its velocity changes and it is deflected through a phenomenon known as refraction. The magnitude of these changes (relative to the speed of light in a vacuum) depends on a characteristic value for each material called the index of refraction, typically denoted by the letter $ n $ (Figure 1). Air has an index of refraction very close to 1.0, while glass typically has an index of refraction near 1.5.

$Figure 1: Refraction at the interface of two materials with n1 < n2. Since the phase velocity is lower in the second medium (v2 < v1), the angle of refraction is smaller than the angle of incidence (θ2 < \ θ1).$

Figure 1: Refraction at the interface of two materials with $ n_1 < n_2 $. Since the phase velocity is lower in the second medium ($ v_1 < v_2 $), the angle of refraction is smaller than the angle of incidence ($ \theta_2 < \theta_2 $).

For light, refraction can be described via Snell's Law, which states that the ratio of the sines of the incident light's angle ($ \theta_1 $) and the angle of refracted light ($ \theta_2 $) is equal to the ratio of the phase velocities ($ \tfrac{v_1}{v_2} $) in the two materials, or equivalently to the indices of refraction ($ \tfrac{n_2}{n_1} $) of the materials:

(1)$$ \frac{\sin{\theta_1}}{\sin{\theta_2}}=\frac{v_1}{v_2} = \frac{n_2}{n_1} $$

where the angles are measured against the normal of the incident surface.

Prisms, lenses, and our own eyes use this refraction to their advantage. By controlling the material (and thus the index of refraction) and the shape of the surface, one can manipulate the direction of light. Prisms can be used to bend a beam of light, and the angle of their surfaces controls the magnitude of these bends (Figure 2). Since prisms are created using flat surfaces, they are only capable of applying a fixed refraction angle on light, regardless of where the light is incident on its surface. A lens, on the other hand, has a curved surface that enables it to focus or diverge collimated light (Figure 3).

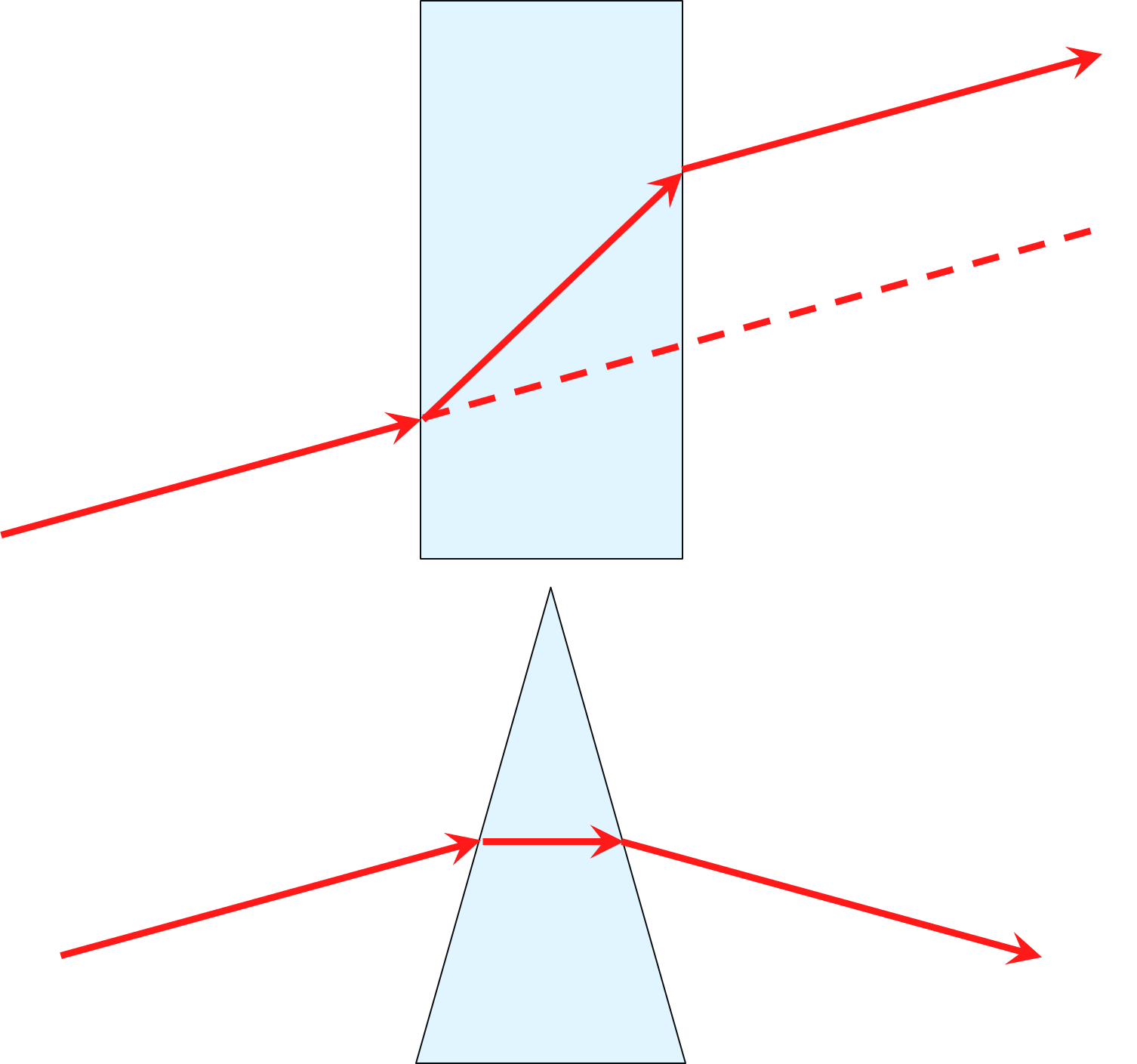
$Figure 2: Top: Light interacting with a medium with parallel sides. The ray is refracted twice with equal angles in opposite directions. The result is a ray that is parallel to the incident ray, only displaced an amount dependent on the element thickness. <strong>(Bottom):</strong> Light interacting with a prism. The light is refracted in the same direction at both interfaces, resulting in a net change in the light's direction.$

Figure 2: (Top):Light interacting with a medium with parallel sides. The ray is refracted twice with equal angles in opposite directions. The result is a ray that is parallel to the incident ray, only displaced an amount dependent on the element thickness. (Bottom): Light interacting with a prism. The light is refracted in the same direction at both interfaces, resulting in a net change in the light's direction.

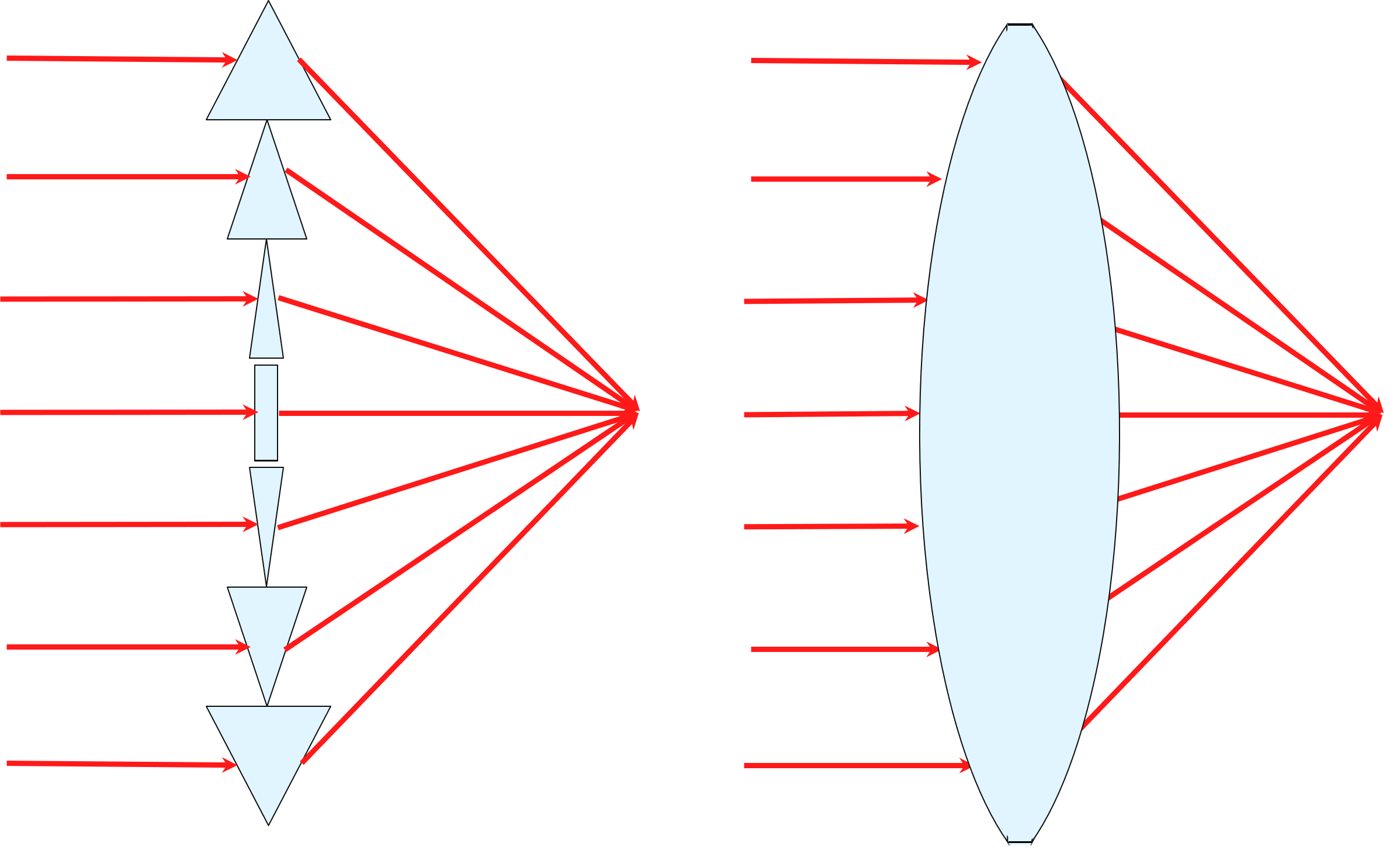
Figure 3: A lens (right) can often be thought of as a series of prisms (left).

The simplest type of lens is also the most common: one whose surface(s) have constant radius of curvature and therefore resembles a section of a sphere. Relative to more complex geometries, these spherical lenses are easy to specify, design, and manufacture.

Spherical surfaces can come in one of two forms: concave, where material is removed so that the surface is hallowed out or rounded inward, and convex, where the surface is rounded outward as in Figure 3. Convex lenses focus collimated light down to a real point called the focal point. Concave lenses diverge incident light (though they do have a virtual focal point).